Quantum Simulator
Quirk is an open-source drag-and-drop quantum circuit simulator for exploring and understanding small quantum circuits. It's a 16-qubit simulator designed to help visualize quantum circuits in a way that's easy to manipulate and fun to play with.
In previous blogs, I've shown circuits that I've made in quirk, like my blog on Quacking, the Art of Quantum Hacking. Here I will be using this blog to show some of my skills that I've picked up from different books I've read, one of which being Programming Quantum Computers: Essential Algorithms and Code Examples by Johnston, Harrigan, and Gemino-Segovia.
One of the things that has interested me lately has been quantum computational mathematics, or using quantum computers to perform mathematic operations. Below are a few examples.
Here we can see that we can use the properties of superposition to create the values \(\ket{0}, \ket{1}, \ket{2}, \ket{3}\) and increment them using Controlled-Not operations to the values of \(\ket{1}, \ket{2}, \ket{3}, \ket{4}\) respectively. We can also do the same with decrementation by reversing the Controlled-Not circuit.
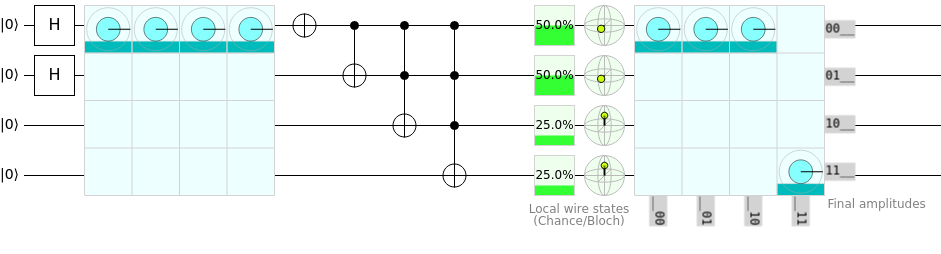
See here we get what we would expect with a classical computer, which is an overflow. Decrementing from \(\ket{0}, \ket{1}, \ket{2}, \ket{3}\) we receive the values of \(\ket{15}, \ket{0}, \ket{1}, \ket{2}\) respectively. Subtracting \(1\) from \(0\) is where we receive the \(15\), with a binary value of \(1111\), which happens to be an overflow from the register we gave to the system.
Using these controls, we can perform basic arithmetic, from addition to subtraction as well as multiplication and exponentiation, which are things we should expect of a classical computer; therefore, we should also expect these computations should also be able to be performed on a quantum computer. Each of these controls in one way or another may be mapped to a set of classical gates if the laws of physics will allow it.



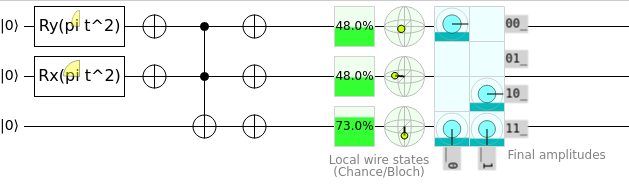
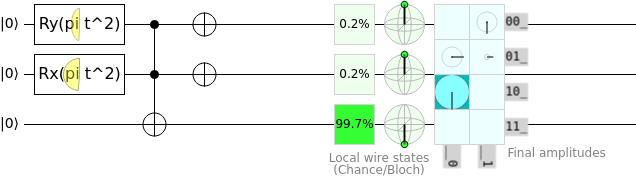
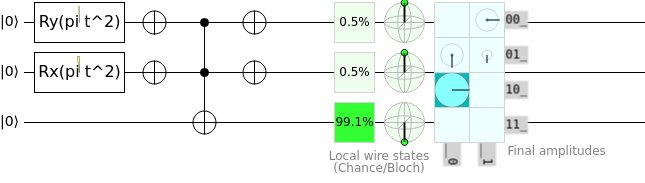
For example, a set of CNOT (Controlled-Not) gates may be used to perform an \(XOR\) operation on a register or compute the absolute value of a given qubit register. We can also see \(NOT\) and \(AND\) operations can be performed similarly to how they would be performed on a classical computer; therefore, any arithmetic that can be performed on a classical computer can theoretically be performed on a quantum computer so long as we do no violate the No Cloning or No Communication theorems.
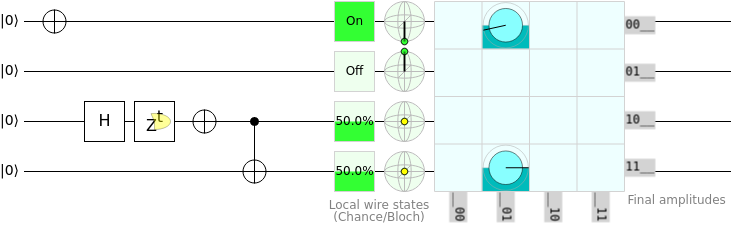
Here we can see that we can conditionaly add values using superposition. In this quantum circuit, we can have the value be both \(\ket{1}\) and \(\ket{5+8}\), which is equal to \(\ket{13}\). Notice that we only add the \(4\)th qubit while the value is \(\ket{5}\), but while the value is also \(\ket{1}\) we do not apply the addition operation. This is known as quantum integer arithmetic.
We can see more arithmetic taking place in the circuit below.
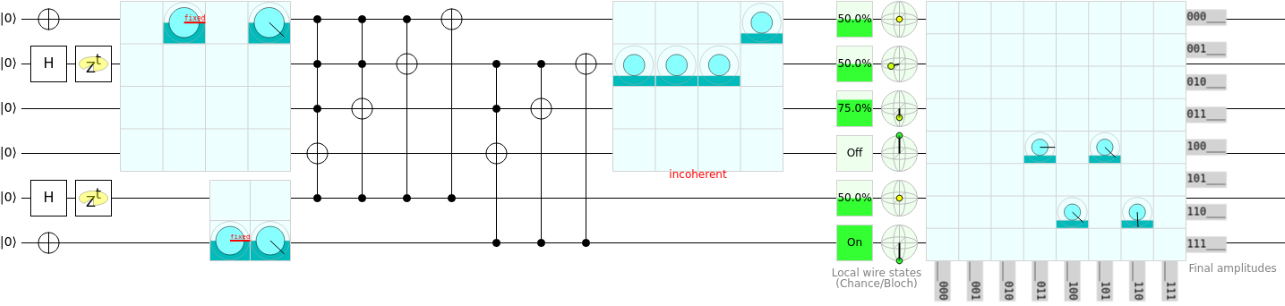
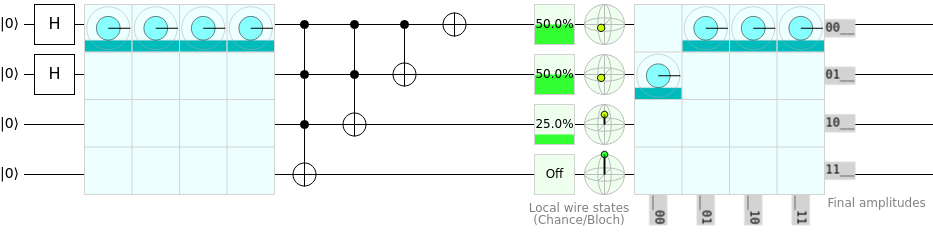
Here, if we treat the first \(4\) qubits as being Register 1, and the last \(2\) qubits as being Register 2, we can represent multi-register arithmetic with \(6\) collective qubits. In the first register, we have a superposition of both \(\ket{1}\) and \(\ket{3}\), and \(\ket{2}\) and \(\ket{3}\) in the second register. By running this circuit we create a scenario in which we are setting the first register equal to itself plus the second register; therefore, we have a superposition of four values: \(\ket{3}, \ket{4}, \ket{5},\) and \(\ket{6}\), each having a 25% chance of being measured out in the first register space.
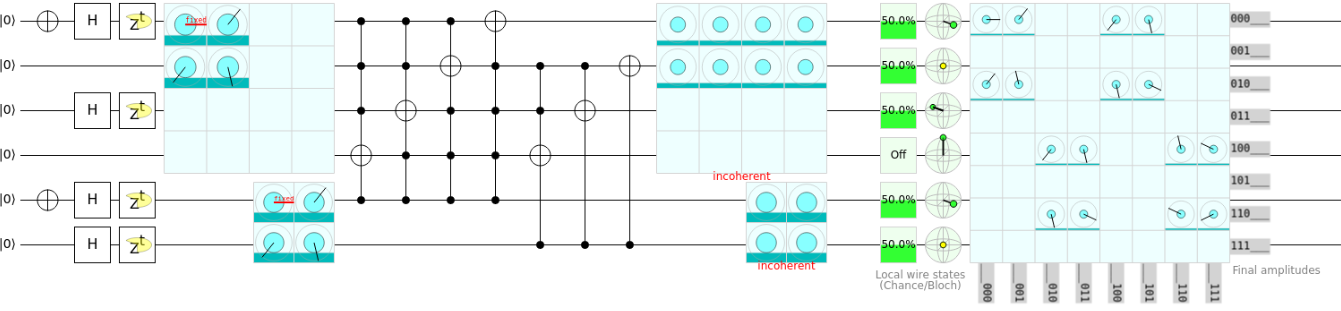
Here is another example, where we start with a register of \(\ket{0}, \ket{1}, \ket{4},\) and \(\ket{5}\), and we add the register \(\ket{0}, \ket{1}, \ket{2},\) and \(\ket{3}\). What we end up with is the combination of possible mathematics of these superpositions.
0. \(\ket{0} + \ket{0} = \ket{0}\)
1. \(\ket{0} + \ket{1} = \ket{1}\) and \(\ket{1} + \ket{0} = \ket{1}\)
2. \(\ket{1} + \ket{1} = \ket{2}\) and \(\ket{1} + \ket{1} = \ket{2}\)
3. \(\ket{1} + \ket{2} = \ket{3}\) and \(\ket{0} + \ket{3} = \ket{3}\)
4. \(\ket{1} + \ket{3} = \ket{4}\) and \(\ket{4} + \ket{0} = \ket{4}\)
5. \(\ket{4} + \ket{1} = \ket{5}\) and \(\ket{5} + \ket{0} = \ket{5}\)
6. \(\ket{4} + \ket{2} = \ket{6}\) and \(\ket{5} + \ket{1} = \ket{6}\)
7. \(\ket{4} + \ket{3} = \ket{7}\) and \(\ket{5} + \ket{2} = \ket{7}\)
8. \(\ket{5} + \ket{3} = \ket{8}\)
We can see from this that we have \(9\) separate superpositions in our outcomes, with \(\ket{0}\) and \(\ket{8}\) having a 6.25% probability each of being measured out, while \(\ket{1}, \ket{2}, \ket{3}, \ket{4}, \ket{5}, \ket{6}, \) and \(\ket{7}\) each have a 12.5% probability of being measured out. These superpositions allow us to do multiple arithmetic at the same time before measurement takes place, which would destroy our previous quantum information.

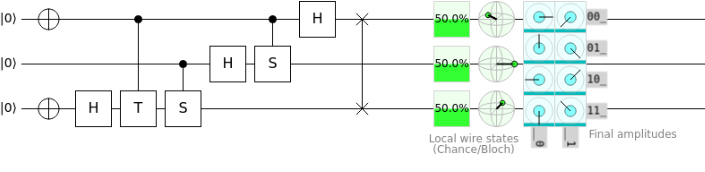
Here we can see a quantum teleportation gate as I had discussed briefly in Quacking, the Art of Quantum Hacking. The purpose of a teleportation gate is to move an infinite amount of information from one qubit space to another qubit space. In this case, we're moving all of the quantum information from qubit one to qubit three.
We start by placing the ancilla qubit (qubit two) and our destination qubit (qubit three) into a Bell State by placing one of them into superposition and entangling them with a CNOT (Controlled-Not) gate. We then take the qubit we are teleporting and apply a CNOT from that qubit to the ancilla qubit. By doing this we have shared information about the rotation with the entangled Bell system. From here, we pass the teleporting qubit through Hadamard and measure out both the teleporting qubit and the ancilla bit.
Now our third qubit can exist in one of four states, but only one of them is correct. To find which one is correct, we need to apply gates to the qubit conditionally based off the measurement outputs of the first couple of qubits. If the first qubit is \(1\), we want to apply a Pauli-Z rotation to the qubit, and if the second qubit is \(1\), we want to apply a Pauli-X rotation to the qubit. In doing this, we solve the four possible qubit state problem discussed earlier and successfully teleport our qubit.
The Quantum Fourier Transform (QFT) is essential for Shor's factoring algorithm and quantum phase estimation. As described on Qiskit's website, the discrete Fourier transform acts on a vector \((x_0, ..., x_{N-1})\) and maps it to the vector \((y_0, ..., y_{N-1})\) according to the formula
$$y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}x_j\omega_N^{jk}$$
where \(\omega_N^{jk} = e^{2\pi i \frac{jk}{N}}\).
The quantum Fourier transform (QFT) transforms between two bases, the computational (Z) basis, and the Fourier basis. The H-gate is the single-qubit QFT, and it transforms between the Z-basis states \(|0\rangle\) and \(|1\rangle\) to the X-basis states \(|{+}\rangle\) and \(|{-}\rangle\). In the same way, all multi-qubit states in the computational basis have corresponding states in the Fourier basis. The QFT is simply the function that transforms between these bases.
$$ |\text{State in Computational Basis}\rangle \quad \xrightarrow[]{\text{QFT}} \quad |\text{State in Fourier Basis}\rangle $$$$ \text{QFT}|x\rangle = |\widetilde{x}\rangle $$
(We often note states in the Fourier basis using the tilde (~).
What we can take from this is that the Quantum Fourier Transform is a linear transformation on quantum bits. So what is a linear transformation? A linear transformation is a mapping \(X \rightarrow Y\) between two vector spaces (sets of vectors) that preserves the operations of vector addition and scalar multiplication.
Equivalently, the quantum Fourier transform can be viewed as a unitary matrix (or a quantum gate, similar to a Boolean logic gate for classical computers) acting on quantum state vectors, where the unitary matrix \(F_N\) is given by
$$ F_N = \frac{1}{\sqrt{N}} \begin{bmatrix} 1 & 1 & 1 & 1 & ... & 1 \\ 1 & \omega & \omega^2 & \omega^3 & ... & \omega^{N-1} \\ 1 & \omega^2 & \omega^4 & \omega^6 & ... & \omega^{2(N-1)} \\ 1 & \omega^3 & \omega^6 & \omega^9 & ... & \omega^{3(N-1)} \\ \vdots & \vdots & \vdots & \vdots & & \vdots \\ 1 & \omega^{N-1} & \omega^{2(N-1)} & \omega^{3(N-1)} & ... & \omega^{(N-1)(N-1)}\end{bmatrix}$$
where \(\omega = \omega_N\). We get, for example, in the case of \(N = 2^2\) and phase \(\omega = i\) the transformation matrix
$$ F_4 = \frac{1}{2} \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & i & 1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & 1 & i \end{bmatrix}$$
This is the most commonly seen unitary matrix to represent QFT's among college examples because it represents the functionality of the QFT without making it too large. We can use this to pass two qubits as a system through the unitary matrix and receive a corresponding output.
One of my favorite things about quantum networking is the ability to detect spies on a network using a circuit designed specifically to add a layer of complexity such that there is an increasing percent chance that a spy will be detected on a network. This is done by applying randomly assumed gates to a quantum spy bit and sending it to the recipient, who randomly applies a gate to their receieved qubit. Upon measuring the output of their randomness and sharing it with one-another, they have a chance of detecting any given spy on a network. Upon running this circuit several times, the chance of detecting a spy exponentially increases.
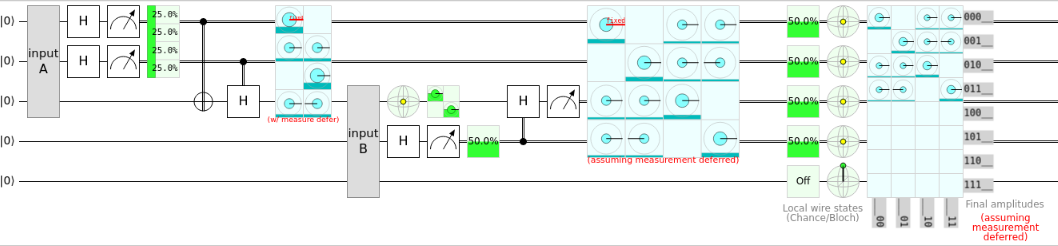
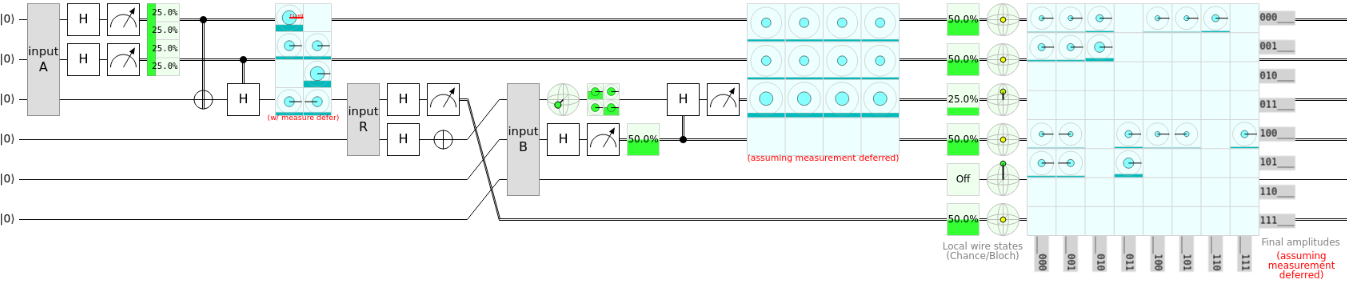
One of the ideas I had was to implant some sort of device on the target's quantum computer such that every time they tried to run the spy circuit, a malicious piece of code would entangle itself with the superpositions created by the TRNG (True Random Number Generator).

By doing this, we could steal the spy bit generator information from the sender and successfully make a copy of our sender's spy bit because we know what gates they would be applying to their qubit.
I think quirk does a wonderful job of keeping the visualization of qubits fluid and easy to read. Despite having its drawbacks in size, it's a wonderful simulator. I actually suggested it to my nine-year-old cousin, Lillie, and she plays around with quantum circuits from time-to-time. I like watching her think as I explain some of the concepts to her as she builds circuits and I explain to her what exactly she's building (even though for the most part she just enjoys watching the spheres rotate around). Hands down, this is my favorite quantum simulator, and I would suggest it to anyone learning quantum computing for the first time.